sqrt(x) in L3

1 A very simple script

We take the textbook definition ¹ of the algorithm for 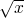, write one function to perform one iteration together with a function to compute the actual error and a function to repeat the iteration until the error is small enough.

For a test, we try to find 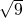using 4 as a starting guess.

# Iteration for sqrt(x):  xkp1 = 1/2 * (xk + x / xk)
def xkp1(x, xk):
    return 1.0 / 2 * (xk + x / xk)
 
# Compute error.
def abserr(x, xk):
    return abs(xk**2 - x)
 
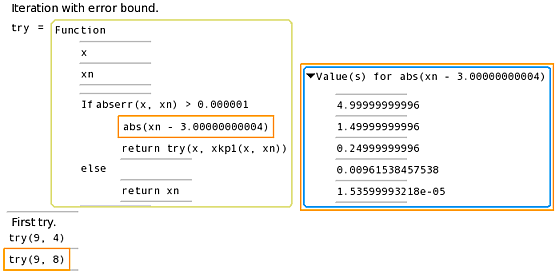
# Iteration with error bound.
def try(x, xn):
    if abserr(x, xn) > 0.0001:
        return try(x, xkp1(x, xn))
    else:
        return xn
 
# First try.
try(9, 4)

Pasting this results in

We run this to get the (value, timestamp) pair

(3.0, 54)

2 Accumulated values

The result seems promising, but we want to see how fast the iteration converged. The term abserr(x, xn) is a natural source of this information, so use insert values as … :

to get a list of computed values:

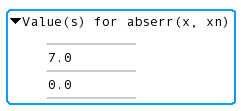
It looks like 4 is a poor starting value, resulting in single-step convergence. We should try a different starting point; paste and append another test

try(9, 8)

and run the program again (L3 only runs the new code) to get

(3.0000153600393218, 264)

or similar.

To only display values produced from try(9, 8), select both abserr(x, xn) and try(9, 8) and use insert values… to get

3 The real error

The values abs(xk**2 - x) are only used to test for some kind of convergence; we really want to see the sequence of values of xn. Use the same selection approach to get them:

In plain text form,

8
4.5
3.25
3.00961538462
3.00001536004

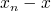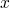Of more interest is the error and its square. We can use the last computed value as the "true" value of , and form the difference in a convenient spot in the same script.

To get extra values to work with, we decrease the error bound to 0.000 001 and re-run the script. As usual, L3 only computes the new value². The last of those values is 3.00000000004; inserting the expression

abs(xn - 3.00000000004)

in the script, re-running it, and inserting the list of these gives the following:

-----------

Footnotes:

¹ This algorithm is chosen to illustrate data selection in L3 only; for a proper implementation of sqrt(), see e.g. http://www.netlib.org/fdlibm/e_sqrt.c

² The first retrieved values are

Showing only data created through:
try(9, 8)
clone id, clone timestamp, value
--------------------------------------------
32864, 91, 8
32931, 136, 4.5
32998, 181, 3.25
33065, 226, 3.00961538462
33132, 271, 3.00001536004

and after replacing the error bound and re-running, the new values retrieved are

32864, 91, 8
32931, 136, 4.5
32998, 181, 3.25
33065, 226, 3.00961538462
33132, 271, 3.00001536004
33292, 349, 3.00000000004

so we can see that the originals are used unchanged.

---